Put a raw egg on a flat table, and give it a good spin with two fingers. The egg spins, however, rather slowly because the liquid inside poorly exchanges momentum with the outside shell. Thus, when you spin the egg by applying force to the shell, most of the inside resists the motion and the friction forces between the inside (immobile) and the shell (mobile) will be slowing down the egg’s speed. But if you consider a cooked egg, proteins contained inside the egg are now forming a solid phase that is tightly joint to the shell. In that case, there are no friction forces in the “egg system” and the movement is not slowed down.
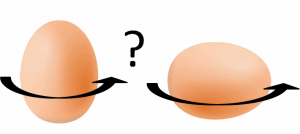
In this case now, the only existing friction forces are those between egg and the support (the table) and the air (which can be reasonably neglected). If your initial momentum transfer is strong enough, you observe a strange phenomenon: the spinning egg starts to rotate upright.
The physical concept used to explain this phenomenon is inertia. Spinning ice skaters can reduce their moment of inertia by pulling in their arms, allowing them to spin faster. You can also sit on a swivel chair and spin on yourself. Extend your arms horizontally and you will slow down. The same is happening with the egg. Friction forces tend to slow down the egg, and decrease overall energy. To save energy, like the skater, the egg stands up and the momentum of inertia consequently decreases.
To spin upright, the egg needs some energy, exactly as one needs some energy to get up in the morning, fighting against gravity. The necessary energy is provided by the rotation itself, and the change of orientation of the egg will only happen if the spinning is fast enough.
— Adrien THUROTTE
Bou-Rabee, N. M., J. E. Marsden, and L. N. Romero, A geometric treatment of Jellett’s egg, Angew. Math. Mech. (ZAMM) 85, (2005), 618-642