There have been already two Questions of the Week about the weather: “Can we control the weather?” (http://junq.info/?p=2783) by Nicola Reusch and “Is accurate weather forecast possible?” (http://junq.info/?p=1318) by myself. Today, I do not want to go into detail about the meteorological work, but demonstrate a mathematical theorem by the means of weather.
You certainly heard about antipodes, i.e. points that lie on diametrically opposite sides on the earth’s surface. If you’d like to have a look where your antipode is at the moment, check refs. [1] and [2]. Now, these two parts of the earth are the farthest apart from each other as you can get, while staying on the ground; with the exemption that they are a little closer, when you are at sea level on both ends than they are when you are on top of Mount Everest on one side. Think about how different the climatic conditions must be between those two antipodal points. What if I told you that at any moment there are at least two antipodal points on earth’s surface which share the same temperature and air pressure. Would you believe me?
No? So too what I thought at first. But let me reveal that it’s true. Take a look at Fig. 1(left). There you see the two antipodes A and B. If we measure the temperature of both points and they are identical, fine, we did our job. But most likely this won’t happen. If we move from the original point A to point B on any path while keeping A and B antipodal points (Fig. 1, middle), the temperatures of the two points will swap (Fig. 1, right). Therefore, there must be at least one set of antipodal points, where the temperature of A and B is identical, since swapping would be impossible otherwise.
Fig. 1: Two antipodal points A and B (left), antipodal paths from A to B (middle), and swapped points A and B (right).
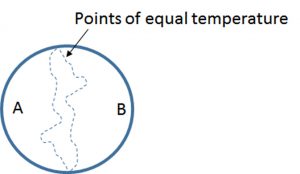
Since swapping will occur on one set of points on a given antipodal path, you can imagine a line separating hemisphere A from hemisphere B on which any pair of antipodes will have equal temperature (Fig. 2). If we check air pressure on one set of antipodal points, we most likely won’t find matching values. But we can also be certain that both values will swap, if we move from one point to the other, while staying on the equal temperature path from Fig. 2.
Fig. 2: Antipodal points on earth’s surface with equal temperature.
Therefore, we must find one pair of antipodes with equal temperature and equal air pressure on earth’s surface at any given moment. Fascinating, isn’t it? This is called the Borsuk-Ulam Theorem.[3] It is a mathematical theorem which remarkably illustrates that results which seem impossible can in fact be true, if you keep investigating in a scientific manner.
–Andreas Neidlinger
References:
[1] https://www.jasondavies.com/maps/antipodes/
[2] http://www.findlatitudeandlongitude.com/antipode-map/#.WB71TfnhCUk
[3] http://www.und.edu/instruct/tprescott/papers/thesis/thesis.pdf