Traffic development
Absolute nothingness ( Śūnyata ) is one of the most exciting notions in Buddhism. Essentially, it cannot be interpreted anyhow but can be thought of as Ultimate Reality[1]. In Mediterranean tradition, ancient cosmologists introduced another term that sounds more familiar – The Chaos. It was associated with the infinite ocean and expressed an initial state of cosmos in potentia[2]. Not to get numb by the immensity of this semantic unit, we can consider chaos as noise having an infinite spectrum of all conceivable frequencies. And through interaction with external conditions, certain modes manage to become more pronounced as, for example, in the process of stimulated emission build-up in the laser[3] or during the process of natural selection in the theory of evolution.[4]
Traffic development
In the context of road traffic development, we can define the situation in ancient times as the initial chaotic state. As there were no roads as such, the traffic was chaotic. With the evolution of horse-drawn transport, the road map was developing. However, the roads were still only directions along which one could get from one place to another.
The situation changed when engine cars jolted the slow and stagnant horse traffic. Between the man and the road there was no middle link anymore that could choose a better way within the given direction on its own. Nonetheless, engine-drawn transport had an obvious advantage of higher achievable speed. In turn, the desire to move faster and faster required less scattering at the surface roughness, which inevitably resulted in roads getting smoother, i.e., less chaotic. In the meantime, the assembly line was progressing drastically and both factors lead to a dense cloud of potentially fast cars. But people were still scratching their heads why the average speed of the road traffic was not increasing. After a while, they figured out who is to blame in the residual scattering – the interaction of the drivers themselves with each other. With the absence of any predefined rules, everyone had to slow down and likely change the direction to avoid physical interaction with another participant of the traffic. Thus, the necessity of the traffic regulations was obvious.
The first “Convention with respect to the international circulation of motor vehicles” was signed in Paris in 1909[5]. Among others, it contained the sign depicted in Fig. 1, which indicated the road intersection. And naturally, originating from the ship traffic, the habitual priority-to-the-right rule was established to regulate the right-of-way for two vehicles with intersecting directions. Later a set of traffic regulations was complemented with priority signs and traffic lights.

Road signs approved at the Paris convention of road traffic.[6]
Gödel’s theorems
In 1930 Kurt Gödel presented two theorems reflecting insuperable limitations of formal arithmetics. These theorems had a direct relation to the second problem from Hilbert’s list asking for the proof that arithmetics is consistent.[7] The first Gödel’s theorem (in Rosser form) states that within any consistent formal system S, one can come up with expression A that can be neither proved nor disproved[8]. In other words, the axiomatic system S is incomplete. Hao Wang published in his Logical Journey[9] the full text that Gödel had written about his discovery of the incompleteness theorems:
“In the summer of 1930 I began to study the consistency problem of classical analysis. It is mysterious why Hilbert wanted to prove directly the consistency of analysis by finitary methods. I saw two distinguishable problems: to prove the consistency of number theory by finitary number theory and to prove the consistency of analysis by number theory <…> Since the domain of finitary number theory was not well-defined, I began by tackling the second half <…> I represented real numbers by predicates in number theory <…> and found that I had to use the concept of truth (for number theory) to verify the axioms of analysis. By an enumeration of symbols, sentences and proofs within the given system, I quickly discovered that the concept of arithmetic truth cannot be defined in arithmetic. If it were possible to define truth in the system itself, we would have something like the liar paradox, showing the system to be inconsistent <…> Note that this argument can be formalized to show the existence of undecidable propositions without giving any individual instances. (If there were no undecidable propositions, all (and only) true propositions would be provable within the syosmos in potestem. But then we would have a contradiction.) <…> In contrast to truth, provability in a given formal system is an explicit combinatorial property of certain sentences of the system, which is formally specifiable by suitable elementary means…”
Traffic regulations in the context of the 1st Gödel’s theorem
We can consider any set of interrelated rules, including traffic regulations, as a formal axiomatic system where each axiom is not subject to prove and serves as a basis for further deriving the formulas and theorems (or behavior in a traffic situation). Clearly, the traffic regulations are consistent because otherwise, the number of car crashes would be much higher. Hence, according to the 1st Gödel’s theorem, the system is incomplete. This means that there would always exist a situation, which cannot be resolved regardless of the number of regulations (axioms) contained in the system.
The example of such a situation can be observed on the road intersection regulated by priority-to-the-right rule depicted in Fig. 2. Here four vehicles coming from every direction want to pass this intersection each going straight. There is no way to resolve this situation (to derive the formula) within the traffic regulations system and the drivers in every certain situation are supposed to make the decision: who has the priority.
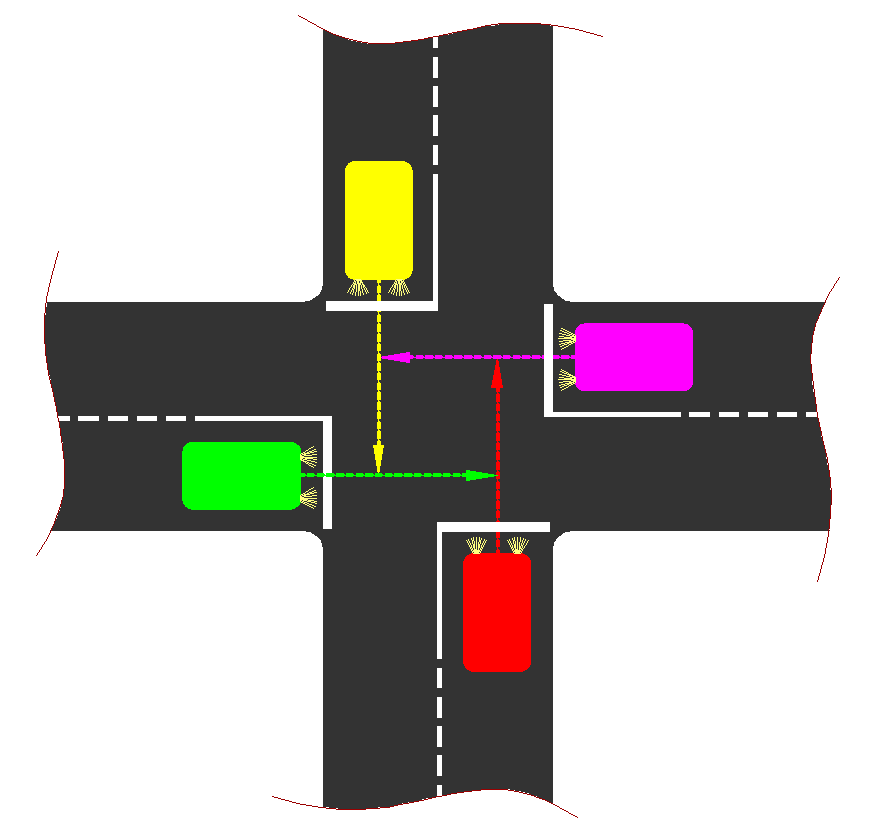
Unresolvable road situation (Sergei Sobolev, CC-BY)
We can incrementally enhance our axiomatic system by introducing another rule to resolve such a dead-end situation. A rule that gives priority to go first, say, to a red car. Again, four red cars on the same road crossing end up with the same confusion. As long as we add the rules (axioms) into the system enumerably, which is the case for the traffic regulations, such situations will always appear. Introducing the priority signs, constant or variable in time, like traffic lights, or topological road junctions (see Fig. 3) can only decrease the probability of this situation emerging.

Topological resolution of left- and right-hand traffic, Pearl River Necklace.[10]
Nowadays, most of the intersections are controlled (or topologically resolved). And let’s assume that the preposterous situation with four red cars trying to figure out the right-of-way on the uncontrolled intersection hasn’t happened up to the moment in our complex but finite system of road traffic. Hence, the drivers’ behavior seems to be fully governed with the traffic regulations. However, there still is a possibility of an unresolvable situation, namely, if one comes up with an expression: “I’m not going to obey the rules. For the axiomatic system of traffic regulations, this expression serves as a “liar paradox” and cannot be resolved. Thus people had to come up with the penalty system for acceptable performance of the traffic regulations. But again, it is impossible to nullify the probability of such a situation emerging.
Instead of conclusion
The aim of this text was not to establish a solid theory in either mathematics or law, and the presented examples may not be in strict compliance with the described statements. However, the author finds entertaining the fact that there are bridges between different islands of knowledge accumulated by mankind over the infinite ocean of the unknown.
— Sergei Sobolev
Read more:
[1] D. Mathers, M. Miller, O. Ando. Self and No-Self: Continuing the Dialogue Between Buddhism and Psychotherapy. 2013 Routledge
[2] http://www.plato.spbu.ru/TEXTS/lebedev/1/ferekid.htm
[3] W. Koechner. Solid-State Laser Engineering, 2006 Springer
[4] C. Darwin. The origin of species by means of natural selection; or, the preservation of favoured races in the struggle for life. 1859 London
[5] Convention with Respect to the International Circulation of Motor Vehicles. The American Journal of International Law Vol. 4, No. 4, Supplement: Official Documents (Oct., 1910), pp. 316-328
[6] https://upload.wikimedia.org/wikipedia/commons/f/f2/1909_Paris_Convention_road_signs.jpg
[7] D. Hilbert. “Mathematical Problems”. Bulletin of the American Mathematical Society. 8 (10): 437–479, 1902.
[8] Introduction to metamathematics. S. Kleene, 1952 D. Van Nostrand Company, Inc.
[9] H. Wang. A Logical Journey. From Gödel to Philosophy. 1996 The MIT Press.
[10] https://www.archdaily.com/64354/pearl-river-necklace-nl-architects/