When Francis Guthrie took on the task to colour a map of England in 1852 he needed four colours to ensure that no neighbouring shires had the same colour. Is this the case for any map imaginable, he wondered.
As it turns out, five colours do suffice, as mathematically proven in 1890 in the five-colour theorem [1]. That indeed four colours are enough to colour a map if every country is a connected region took until 1967 to prove [2] and required computer assistance. It abstracted the idea to geometric graph theory where regions are represented by vertices connected by an edge if they share a border (see fig. 1).
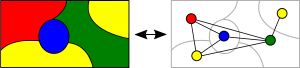
Fig 1: Illustration of the abstraction of the map colouring problem to graph theory.
The four-colour theorem was then proven by demonstrating the absence of a map with the smallest number of regions requiring at least five colours. In its long history the theorem attracted numerous false proofs and disproofs. The simplest versions of counterexamples focus on painting extensive regions that bordering many others, thereby forcing the other regions to be painted with only three colours. The focus on the large region might cause people’s inability to see that colouring the remaining regions with three colours is actually possible.
Even before the four-colour theorem was proven, the abstraction to graph theory evoked the question as to how many colours would be needed to colour a plane so that no two points on that plane with distance 1 do have the same colour. This is also known as the Hadwiger–Nelson problem. Note that we are not colouring continuous areas in this case, but instead each individual point of the plane, rendering it extremely more complex. In the 1950s it was known that this sought number, the chromatic number of the plane, had to be between four and seven.
The upper border is known from the existing tessellation of a plane by regular hexagons that can be seven-coloured [4] (fig. 2). The maximal distance within one hexagon, the diameter, needs to be smaller than one to comply with the requirement. Additionally one needs to ensure that the distance to the next hexagon of the same colour is larger than one. These constraints imply that the hexagon edge length a has to be between 0.5 and $\sqrt(7)/2$ for an allowed colouring of the plane, where no two points with distance one have the same colour.
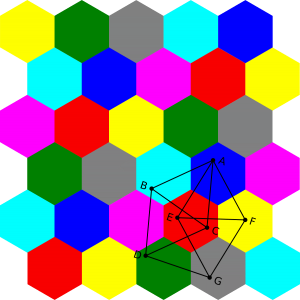
Fig. 2: Colouring of a plane in a seven colour tessellation pattern of regular hexagons.
As to the lower border for the chromatic number of the plane, it is obvious that two colours will not suffice to colour even the simple unit-distance path of an equilateral triangle (see fig. 3 a). To demonstrate that three colours do not suffice either and therefore at least four colours a needed, we take a look at the Moser spindle shown in fig. 3 b. The seven vertices (all eleven edges / connections have unit-distance) cannot be coloured with three colours, say green, blue, and yellow. Assigning green to vertex A, its neighbours B and C need to be blue and yellow, respectively, or vice versa, enforcing D to be green again. A’s other neighbouring vertices E and F analogously are assigned blue and yellow, or vice versa, enforcing in turn G to be green. This conflicts with G’s neighbour D to be green, too, thus demonstrating that arbitrary unit-distance graphs require at least four colours.
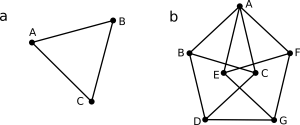
Fig 3: a) An equilateral triangle as a simple example for a unit-distance graph. b) The Moser spindle is a four-colourable unit distance graph [3].

Fig 4: Five-colourable unit distance graph with 533 vertices. The fifth colour (white) is only used in the centre. [6]
— Alexander Kronenberg
[1] Heawood, (1890), “Map-Colour Theorems”, Quarterly Journal of Mathematics 24, pp. 332–338
[2] Appel, Haken, (1989), “Every Planar Map is Four-Colorable”, Contemporary Mathematics 98, With the collaboration of J. Koch., doi:10.1090/conm/098
[3] Soifer, (2009) “The Mathematical Coloring Book”, Springer
[4] Hadwiger, (1945), “?berdeckung des euklidischen Raumes durch kongruente Mengen”, Portugal. Math. 4 ,pp. 238–242
[5] de Grey, (2018), “The chromatic number of the plane is at least 5”, arXiv:1804.02385
[6] Heule, (2018), “Computing Small Unit-Distance Graphs with Chromatic Number 5”, arXiv:1805.12181